SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
문제
N x N 배열 안의 숫자는 해당 영역에 존재하는 파리의 개수를 의미한다.
아래는 N=5 의 예이다.


M x M 크기의 파리채를 한 번 내리쳐 최대한 많은 파리를 죽이고자 한다.
죽은 파리의 개수를 구하라!
예를 들어 M=2 일 경우 위 예제의 정답은 49마리가 된다.
[제약 사항]
1. N 은 5 이상 15 이하이다.
2. M은 2 이상 N 이하이다.
3. 각 영역의 파리 갯수는 30 이하 이다.
[입력]
가장 첫 줄에는 테스트 케이스의 개수 T가 주어지고, 그 아래로 각 테스트 케이스가 주어진다.
각 테스트 케이스의 첫 번째 줄에 N 과 M 이 주어지고,
다음 N 줄에 걸쳐 N x N 배열이 주어진다.
[출력]
출력의 각 줄은 '#t'로 시작하고, 공백을 한 칸 둔 다음 정답을 출력한다.
(t는 테스트 케이스의 번호를 의미하며 1부터 시작한다.)
입력
10
5 2
1 3 3 6 7
8 13 9 12 8
4 16 11 12 6
2 4 1 23 2
9 13 4 7 3
6 3
29 21 26 9 5 8
21 19 8 0 21 19
9 24 2 11 4 24
19 29 1 0 21 19
10 29 6 18 4 3
29 11 15 3 3 29
...
출력
#1 49
#2 159
...
풀이1 : 실패
class Solution {
public static void main(String args[]) throws Exception {
Scanner sc = new Scanner(System.in);
int T;
T=sc.nextInt();
for(int test_case = 1; test_case <= T; test_case++) {
int N = sc.nextInt();
int M = sc.nextInt();
int[][] flies = new int[N][N];
for (int i = 0; i < N * N; i++) {
int x = i % N;
int y = i / N;
flies[y][x] = sc.nextInt();
}
System.out.println("#" + test_case + " " + calculate(flies, N, M));
}
}
private static int calculate(int[][] flies, int N, int M) {
int index = N - M;
int count = 0;
for (int i = 0; i < index; i++) {
for (int j = 0; j < index; j++) {
count = Math.max(count, sum(flies, i, j, M));
}
}
return count;
}
private static int sum(int[][] flies, int startX, int startY, int M) {
int sum = 0;
for (int y = startY; y < startY + M; y++) {
for (int x = startX; x < startX + M; x++) {
sum += flies[y][x];
}
}
return sum;
}
}- 4중 for문
- 효율적이지 못할 뿐더러 테스트 10개 중 5개 통과
풀이2
참고
[JAVA] SWEA 2001 파리잡기 (누적합)
<입력>25 21 3 3 6 78 13 9 12 84 16 11 12 62 4 1 23 29 13 4 7 36 329 21 26 9 5 821 19 8 0 21 199 24 2 11 4 2419 29 1 0 21 1910 29 6 18 4 329 11 15 3 3
velog.io
[알고리즘/JAVA] 누적 합 (Prefix Sum)
누적합 (Prefix Sum) 배열 또는 리스트 등에서 일정 구간의 합을 빠르게 계산하기 위한 방법이면서 동적 계획법(DP)의 형태 중 하나이다.기본적인 방식은 각 요소까지의 누적 합을 계산하여 이를
sjh9708.tistory.com
class Solution {
public static void main(String args[]) throws Exception
Scanner sc = new Scanner(System.in);
int T;
T=sc.nextInt();
for(int test_case = 1; test_case <= T; test_case++) {
int N = sc.nextInt();
int M = sc.nextInt();
int[][] map = new int[N][N];
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
map[i][j] = sc.nextInt();
}
}
int[][] sumMap = makeSumMap(map, N, M);
int result = getMax(sumMap, N, M);
System.out.println("#" + test_case + " " + result);
}
}
private static int[][] makeSumMap(int[][] map, int N, int M) {
int[][] sumMap = new int[N + 1][N + 1];
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
sumMap[i][j] = map[i - 1][j - 1] + sumMap[i - 1][j] + sumMap[i][j - 1] - sumMap[i - 1][j - 1];
}
}
return sumMap;
}
private static int getMax(int[][] sumMap, int N, int M) {
int max = 0;
for (int i = M; i <= N; i++) {
for (int j = M; j <= N; j++) {
max = Math.max(max, sumMap[i][j] - sumMap[i - M][j] - sumMap[i][j - M] + sumMap[i - M][j - M]);
}
}
return max;
}
}- 누적합 알고리즘 사용
// 누적합 알고리즘
sumMap[i][j] = map[i-1][j-1] + sumMap[i-1][j] + sumMap[i][j-1] - sumMap[i-1][j-1]
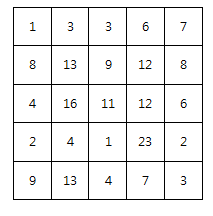
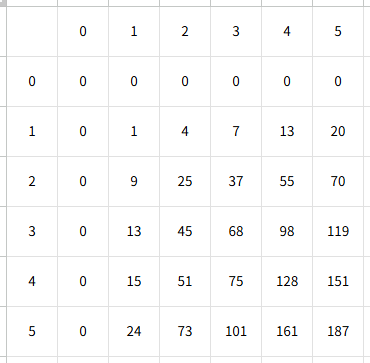
왼쪽의 예시를 누적합 2차원 배열로 바꾸면 오른쪽과 같이 된다.
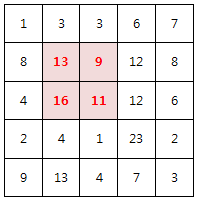
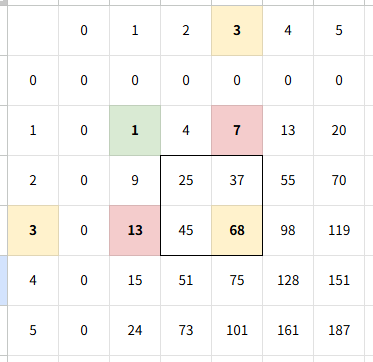
이 때, 해당 칸의 합을 구하려면 다음과 같이 계산해야 한다.
왼쪽 표에서 표시된 사각형의 오른쪽 아래의 좌표는 (2, 2)이다.
오른쪽 표는 0으로 채워진 부분이 있기 때문에 한 칸씩 옮겨 (3, 3)을 찾아야 한다.
(3, 3)의 값인 68은 왼쪽 표의 (0, 0)부터 (2, 2)까지의 누적합이다. 그렇기에 필요없는 값은 빼주어야 한다.
M이 2이기에, 왼쪽으로 2만큼 움직여 (3, 1)의 값인 13을 찾아 뺀다. 이는 왼쪽 표의 (0, 0)부터 (3, 0)까지인 1, 8, 4의 합과 같다.
이번엔 위로 2만큼 움직여 (1, 3)의 값인 7을 찾아 뺀다. 이는 왼쪽 표의 (0, 0)부터 (0, 3)까지인 1, 3, 3의 합과 같다.
이 때 (0, 0)의 값이 2번 계산되기에 한 번 더해주어야 한다. (1, 1)을 찾아 그 값인 1을 다시 더해준다.
정리하자면, 68 - 13 - 7 + 1 = 49 라는 계산이 된다.
쉬운 문제라고 생각했지만, 생각보다 잘 풀리지 않았다. 그래도 새로운 알고리즘을 알게 되었다.
'JAVA > Coding Test Study' 카테고리의 다른 글
| [D2] SWEA - 1974. 스도쿠 검증 : Java (1) | 2024.11.14 |
|---|---|
| [D2] SWEA - 1204. [S/W 문제해결 기본] 1일차 - 최빈수 구하기 : Java (0) | 2024.10.25 |
| [D2] SWEA - 1954. 달팽이 숫자 : Java (0) | 2024.10.25 |
| [D2] SWEA - 1859. 백만 장자 프로젝트 : Java (1) | 2024.10.25 |
| [Easy] LeetCode - no.530 Minimum Absolute Difference in BST : Java (1) | 2024.10.25 |

